本文共 7693 字,大约阅读时间需要 25 分钟。
目录
1、网络架构
openvswitch与linux-bridge相比较而言,openvswitch支持的网络类型更加丰富,应用也比较广泛,因此图示直接使用OVS。linux-bridge支持local, flat, vlan和vxlan 四种network type,目前不支持gre,相比较而言openvswitch支持GRE网络;
OpenStack 至少包含下面几类网络流量
- Management:节点之间 message queue 内部通信以及访问 database 服务;
- API:通过该网络向用户暴露 API 服务;(下图中API网络和管理网络合为一体)
- VM:VM 网络由 Neutron 配置和管理;
- External:External 网络指的是 VM 网络之外的网络,该网络不由 Neutron 管理;
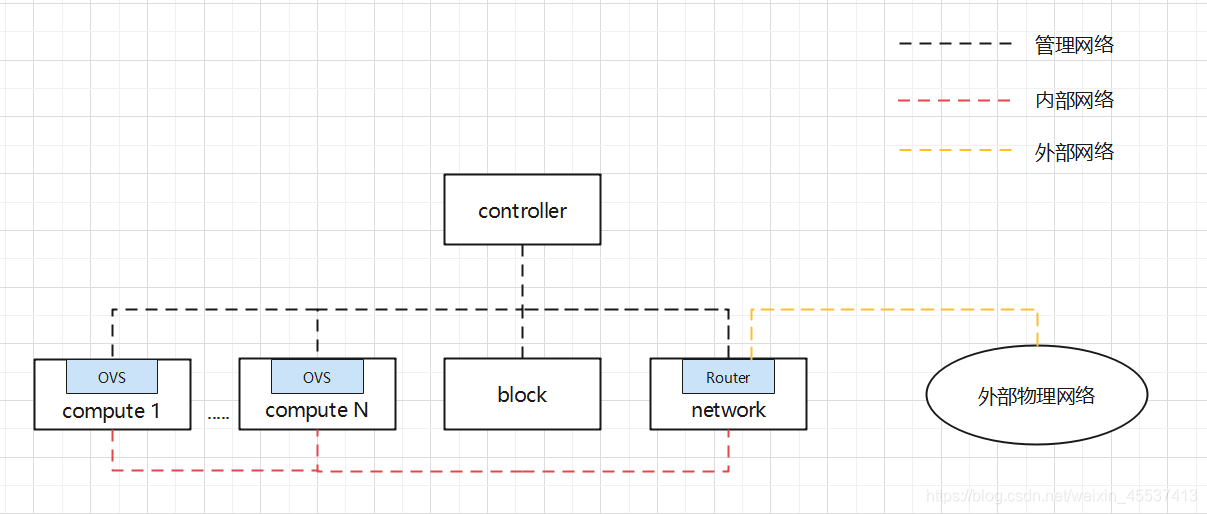
管理网络:用户管理所有节点的网络;
内部网络:计算节点与网络节点通过内部网络通信,tenant network(租户网络,租户自己创建管理,网络之间可以重合);
外部网络:内部的VM与外部物理网络间使用外部网络通信使用,一般由管理员创建并赋予相应属性,称为public network(或者叫provider network?);
2、neutron模块
主要包含以下几个部分:
(1)neutron-server:可以理解为类似于nova-api那样的一个组件,一个专门用来接收neutron REST API调用的服务器。负责将不同的rest api发送到不同的neutron-plugin。接受和路由API请求到网络plug-in。一般部署在控制节点(controller),负责通过Neutron-server响应的API请求;
(2)neutron-plugin:可以理解为不同网络功能(例如创建端口(ports)、网络(Networks)、子网(Subnets)等)实现的入口,现在大部分都是软件定义网络,各个厂商都开发自己的plugin(插件)。neutron-plugin接收netron-server发过来的rest api,向neutron database完成一些信息注册(比如用户要建端口)。然后将具体要执行的业务操作和参数通知给自身对应的neutron-agent。Openstack的plug-ins一般支持Open vSwitch、Linux Bridging、思科物理/虚拟交换机等等。一般Core plugin 和service plugin已经集成到neutron-server中,不需要运行独立的plugin服务。
(3)agent:常见的agent包括L3、DHCP、plug-in agent;一般网络节点需要部署Core Plugin的代理和service Plugin的代理,计算节点也需要部署Core Plugin的代理,通过该代理才能建立二层连接。
(4)messaging queue:在neutron-server和agents之间路由信息,同时作为一个数据库存储plug-ins的网络状态;
模块之间调用关系:(此段为摘抄内容)
(5)Client(客户端)是指使用Neutron服务的应用程序,可以是命令行工具(脚本)、Horizon和Nova计算服务等;
(6)Neutron-database(数据库,默认使用MariaDB)用于存放OpenStack的网络状态信息,包括网络、子网、端口、路由器等;
(7)network provider:提供网络服务的物理或者虚拟网络设备,例如 Linux Bridge,Open vSwitch 或者其他支持 Neutron 的物理交换机;
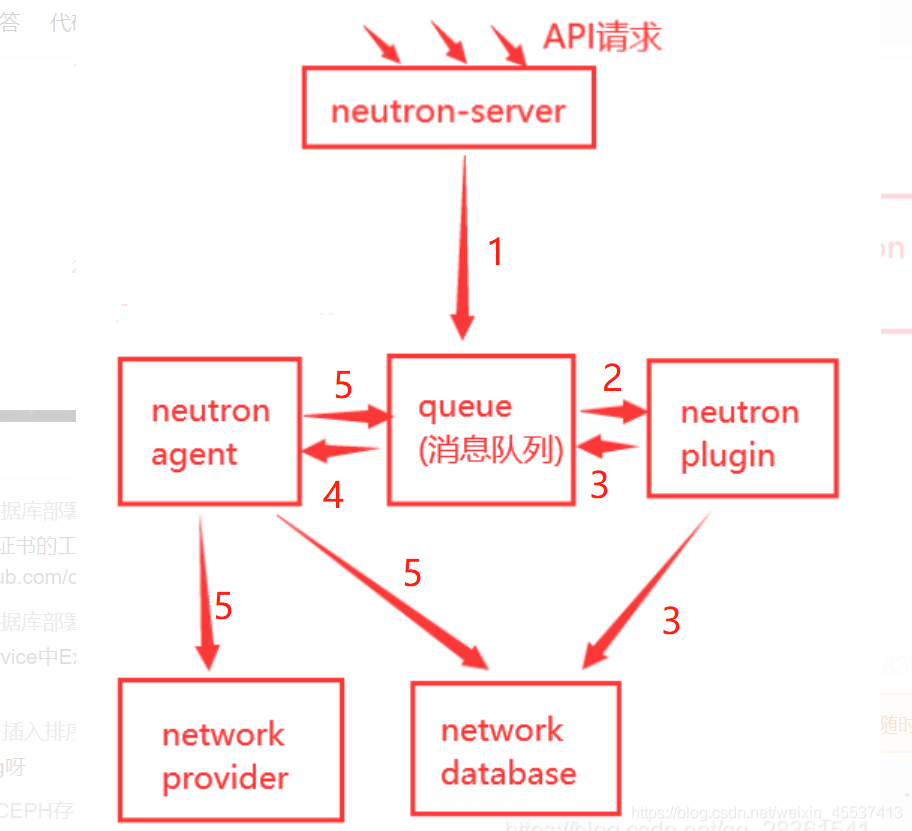
举列说明:创建一个Vlan 10虚拟网络的流程。
- 1、Neutron-server 收到创建网络(Network) 的请求,通过消息队列(RabbitMQ)通知已注册的Linux Bridge插件,这里架设网络提供者为Linux Bridge。
- 2、该插件将要创建的网络信息(如名称、ID值、VLANID等)保存到数据库中并通过消息队列通知运行在各个节点上的代理。
- 3、代理收到信息后会在节点上物理网卡上创建Vlan设备(比如物理接口的子接口 Eth1.10),并创建一个网桥(比如brgXXX)来桥接网络设备。
2.1 plugin
几点说明:
- plugin 解决的是 What 的问题,即网络要配置成什么样子?而至于如何配置 How 的工作则交由 agent 完成。
- plugin,agent 和 network provider 是配套使用的,如果network provider用的linux bridge则使用对应的plugin和agent,若是使用的OVS则使用OVS的plugin和agent;
- plugin 的一个主要的职责是在数据库中维护 Neutron 网络的状态信息。通过ML2(Modular Layer 2)plugin,各种 network provider 无需开发自己的 plugin,只需要针对 ML2 开发相应的 driver 就可以了;
- plugin 按照功能分为两类: core plugin 和 service plugin。core plugin 维护 Neutron 的 netowrk, subnet 和 port 相关资源的信息,与 core plugin 对应的 agent 包括 linux bridge, OVS 等; service plugin 提供 routing, firewall, load balance 等服务,也有相应的 agent。
2.2 agent
| agent | 描述 |
| L3 agent (neutron-l3-agent) | 提供L3/NAT转发,使租户内的虚机实例被外部网络访问 |
| dhcp agent (neutron-dhcp-agent) | 为租户网络提供dhcp功能 |
| metering agent (neutron-metering-agent) | 提供L3数据流量的监控、计算 |
| metadata agent | 是提供一个机制给用户,可以设定每一个instance 的参数 |
| OpenvSwitch agent | 使用Open vSwitch来实现VLAN, GRE,VxLAN来实现网络的隔离,还包括了网络流量的转发控制 |
| plug-in agent ( neutron-*-agent ) | 在每个hypervisor上运行以执行本地vSwitch配置。 这个插件是否运行取决于使用的插件,有些插件不需要代理。 |
| neutron-lbaas-agent | 提供LB的服务 |
| neutron-firewall-agent | 提供防火墙服务 |
2.3 neutron的两种部署方式
core plugin和service plugin都已集成到neutron server中,不需要单独部署。
方式一:控制节点+计算节点
- 控制节点:部署的服务包括:neutron server, core plugin 的 agent 和 service plugin 的 agent;
- 计算节点:部署 core plugin 的agent,负责提供二层网络功能;
说明:(1)控制节点和计算节点都需要部署 core plugin 的 agent,因为通过该 agent 控制节点与计算节点才能建立二层连接;(2)可以部署多个控制节点和计算节点;
方式二:控制节点+网络节点+计算节点
- 控制节点:部署的服务包括:neutron server;
- 网络节点:core plugin 的 agent 和 service plugin 的 agent;
- 计算节点:部署 core plugin 的agent,负责提供二层网络功能;
说明:方式二更适合大规模的openstack环境,控制与网络节点分离开,控制节点只通过neutron server响应API请求,然后调用网络节点的plugin插件;网络节点单独拿出来负责数据的交换,路由以及 load balance等高级网络服务。
2.4 neutron server
整体架构:neutron=API+plugin
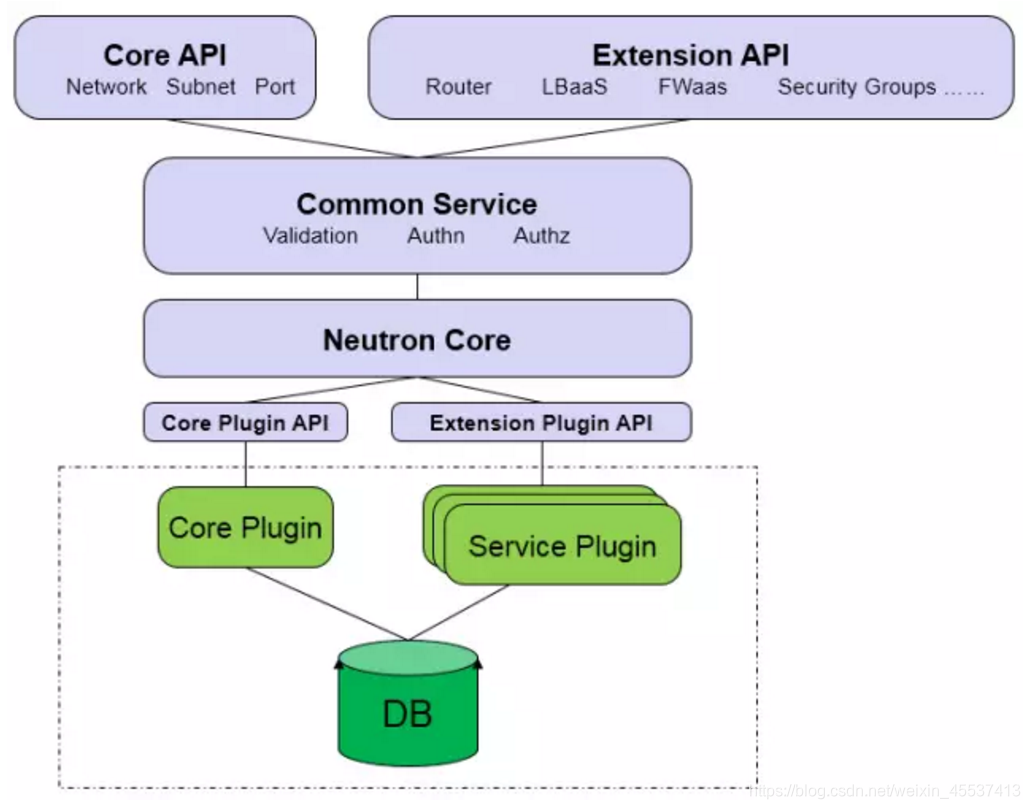
- Core API:对外提供管理 network, subnet 和 port 的 RESTful API。
- Extension API:对外提供管理 router, load balance, firewall 等资源 的 RESTful API。
- Commnon Service:认证和校验 API 请求。
- Neutron Core:Neutron server 的核心处理程序,通过调用相应的 Plugin 处理请求。
- Core Plugin API:定义了 Core Plgin 的抽象功能集合,Neutron Core 通过该 API 调用相应的 Core Plgin。
- Extension Plugin API:定义了 Service Plgin 的抽象功能集合,Neutron Core 通过该 API 调用相应的 Service Plgin。
- Core Plugin:实现了 Core Plugin API,在数据库中维护 network, subnet 和 port 的状态,并负责调用相应的 agent 在 network provider 上执行相关操作,比如创建 network。
- Service Plugin:实现了 Extension Plugin API,在数据库中维护 router, load balance, security group 等资源的状态,并负责调用相应的 agent 在 network provider 上执行相关操作,比如创建 router。
调用关系:通过仪表盘/脚本/Nova调用plugin,plugin再调用对应的agent;
neutron网络的开放性:支持多种network provider。只需要不同的netwrok provider开发出对应的plugin和agent既可。但弊端是(1)只能在 OpenStack 中使用一种 core plugin;(2)不同plugin之间代码重复率高,开发难度大。ML2 Core Plugin解决了传统Core Plugin的这个问题。
2.4.1 ML2 Core Plugin
使用ML2 Core Plugin的需求是:(1)传统Core Plugin无法同时提供多种network provider;(2)开发工作量大。
采用 ML2 plugin 后,可以在不同节点上分别部署 linux bridge agent, open vswitch agent, hyper-v agent 或其他第三方 agent。ML2 不但支持异构部署方案,同时能够与现有的 agent 无缝集成:以前用的 agent 不需要变,只需要将 Neutron server 上的传统 core plugin 替换为 ML2。
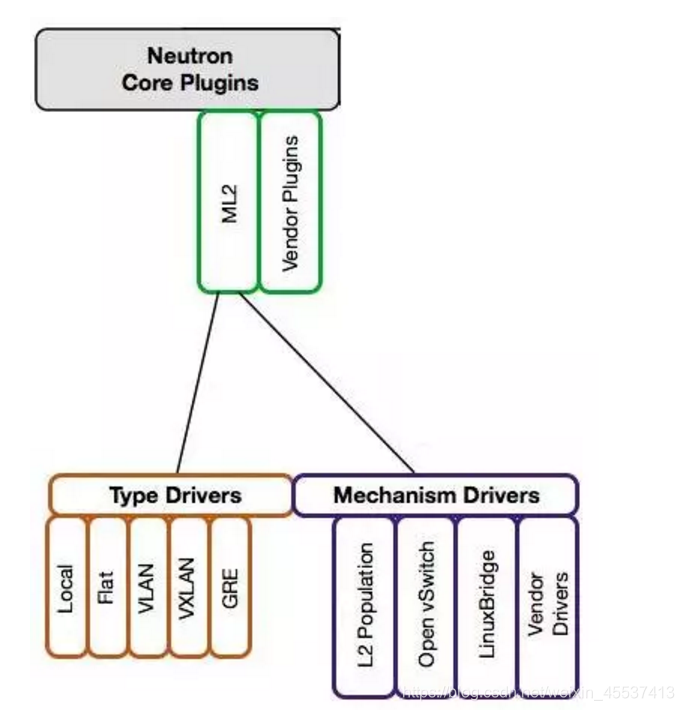
ML2 对二层网络进行抽象和建模,引入了 type driver 和 mechansim driver。type driver 负责维护网络类型的状态,执行验证,创建网络等,支持vlan、vxlan、gre、flat、local网络;mechanism driver 负责获取由 type driver 维护的网络状态,并确保在相应的网络设备(物理或虚拟)上正确实现这些状态。
mechanism driver 有三种类型:(1)Agent-based:包括 linux bridge, open vswitch 等。(2)Controller-based:包括 OpenDaylight, VMWare NSX 等。(3)基于物理交换机;此外,涉及L2 population driver,其作用是优化和限制 overlay 网络中的广播流量。
2.4.2 Service Plugin / Agent
C:net, subnet 和 port。而对于更高级的网络服务(防火墙、router、LB等),则由 Service Plugin/Agent 管理。
- DHCP:dhcp agent 通过 dnsmasq 为 instance 提供 dhcp 服务;
- Routing:l3 agent 可以为 project(租户)创建 router;
- Firewall:l3 agent 可以在 router 上配置防火墙策略;
- Load Balance:Neutron 默认通过 HAProxy 为 project 中的多个 instance 提供 load balance 服务;
2.4.3 neutron架构的小结
如下图:
- Neutron server 接收 api 请求。
- plugin/agent 实现请求。
- database 保存 neutron 网络状态。
- message queue 实现组件之间通信。
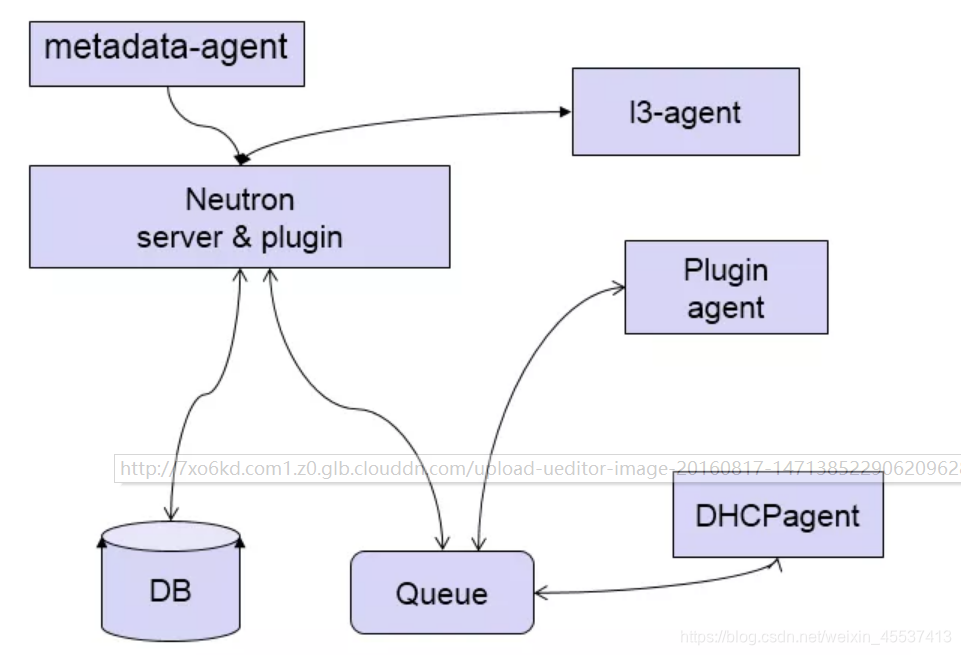
更深入的理解:
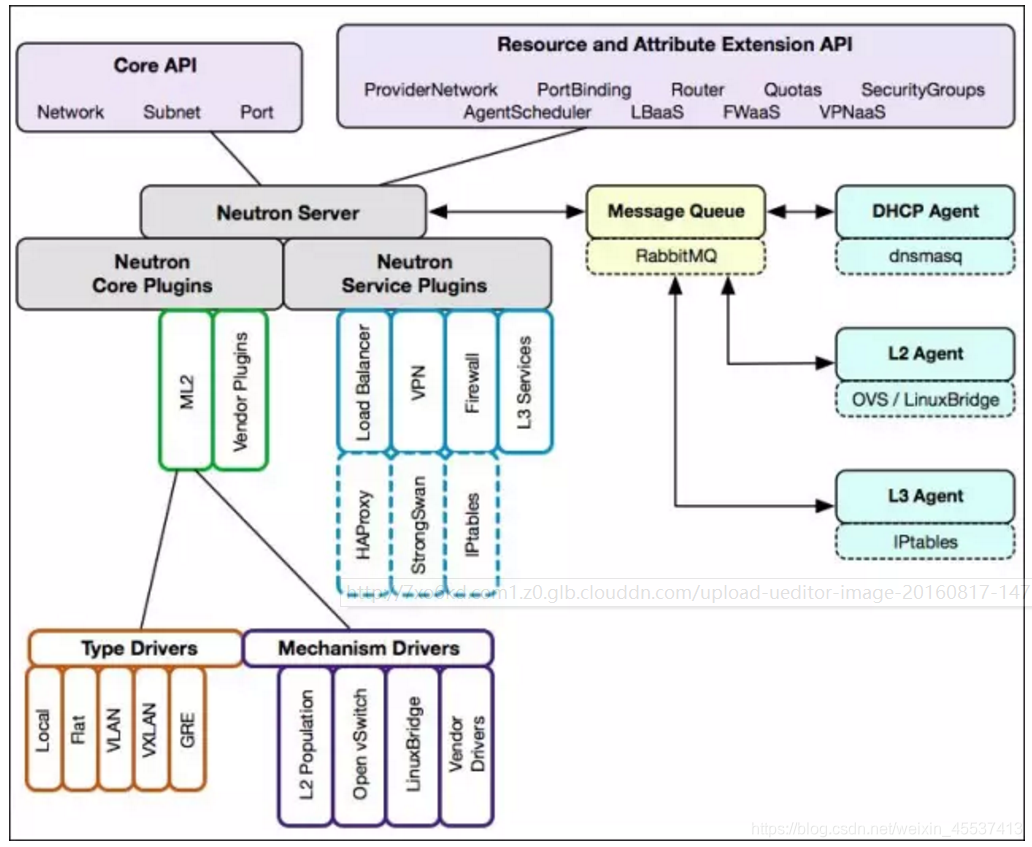
- Neutron 通过 plugin 和 agent 提供的网络服务。
- plugin 位于 Neutron server,包括 core plugin 和 service plugin。
- agent 位于各个节点,负责实现网络服务。
- core plugin 提供 L2 功能,ML2 是推荐的 plugin。
- 使用最广泛的 L2 agent 是 linux bridage 和 open vswitch。
- service plugin 和 agent 提供扩展功能,包括 dhcp, routing, load balance, firewall, vpn 等。
2.5 linux bridge实现neutron网络
2.5.1 linux-bridge mechanism driver
neutron默认使用ml2的service plugin,这个在配置文件有体现:
vi /etc/neutron/neutron.conf[DEFAULT]rpc_backend = rabbitcore_plugin = ml2......
需要在控制节点与计算节点中指定的/etc/neutron/plugins/ml2/ml2_conf.ini的文件中将mechanism_drivers设定为openvswitch或者linux bridge,可以写多个,ML2 会负责加载
[ml2]type_drivers = vlan,vxlantenant_network_types = vlan,vxlanmechanism_drivers = ml2_h3c,openvswitch......
2.5.2 linux bridge中的几种网络设备和网络类型
在 linux bridge 环境中,存在下面的网络设备类型(不同的网络里不一样):
- tap interface命名为 tapN (N 为 0, 1, 2, 3......)
- linux bridge命名为 brqXXXX。
- vlan interface命名为 ethX.Y(X 为 interface 的序号,Y 为 vlan id),存在vlan网络;
- vxlan interface命名为 vxlan-Z(z 是 VNI),vxlan网络;
- 物理 interface命名为 ethX(X 为 interface 的序号)
linux-bridge 支持 local, flat, vlan 和 vxlan 四种 network type,目前不支持 gre。
2.5.3 Local Netwrok
local network 的特点是不会与宿主机的任何物理网卡相连,因此该宿主机上的VM不能与宿主机外部的网络通信,完全隔离。对于每个 local netwrok,ML2 linux-bridge 会创建一个 bridge,instance 的 tap 设备会连接到 bridge。对于同一个bridge,其下的instance属于同一个Local network,每个instance通过各自的tap设备连接到bridge,从可以互相通信。不同bridge之间不能相互通信。网络架构如下图所示:
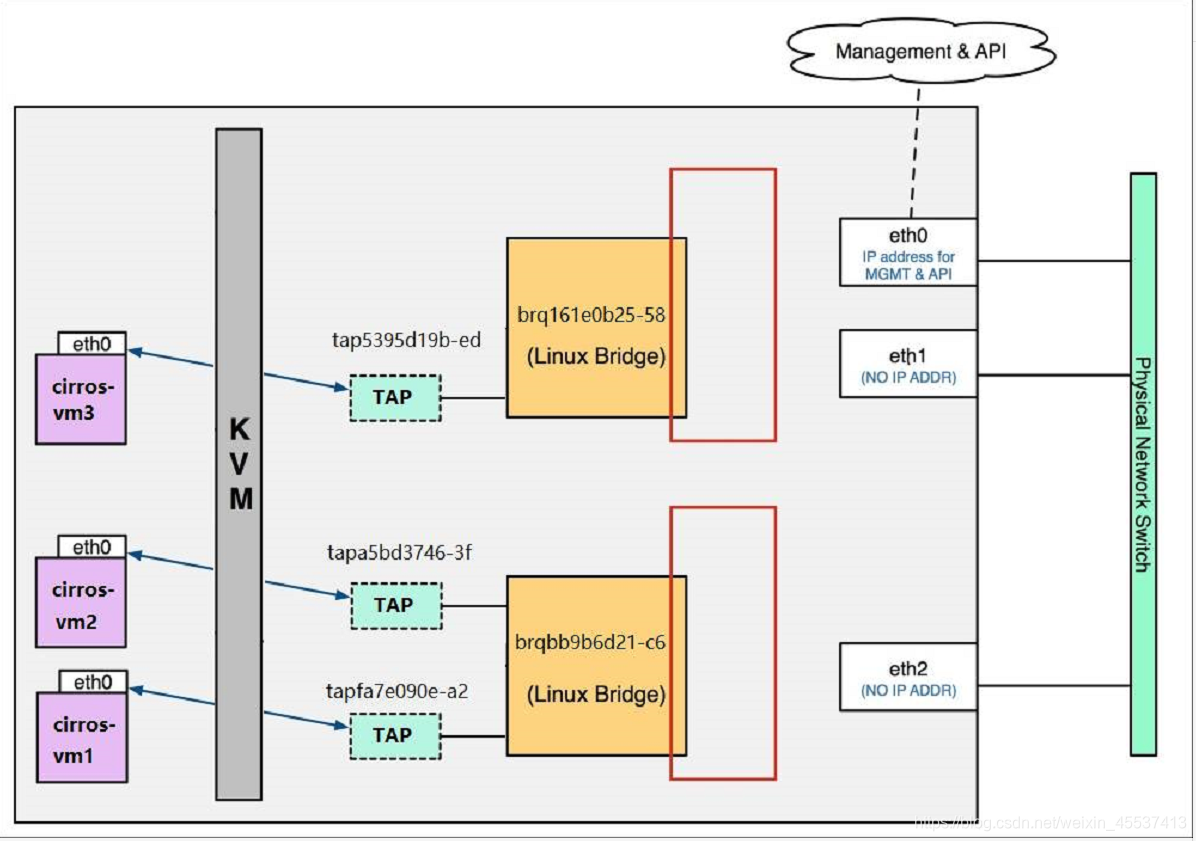
配置文件中需要配置type_drivers的类型有local,/etc/neutron/plugins/ml2/ml2_conf.ini,并设置普通租户创建的网络类型(admin用户可以指定网络类型)
[ml2]type_drivers = vlan,vxlantenant_network_types = vlan,vxlanmechanism_drivers = ml2_h3c,openvswitchextension_drivers = ml2_extension_h3c......
通过WEB GUI创建相应的虚机VM,会自动创建一个port,该port信息包含ip和mac。宿主机根据该port信息创建相应tap设备,tap会关联相应的bridge,同时映射成虚机的虚拟网卡(VIF)。
总结几点:
- 1. 位于同一 local network 的 instance 可以通信。
- 2. 位于不同 local network 的 instance 无法通信。
- 3. 一个 local network 只能位于一个物理节点,无法跨节点。
由于其只限制在单个宿主机中通信,无法跨网络和跨主机,在实际的应用中基本很少用到local network,可以仅作为后续学习复杂网络的基础。
2.5.4 Flat Network
flat network 是不带 tag 的网络,要求宿主机的物理网卡直接与 linux bridge 连接,并且flat network与网卡是一一对应的关系,网络架构如下图所示。
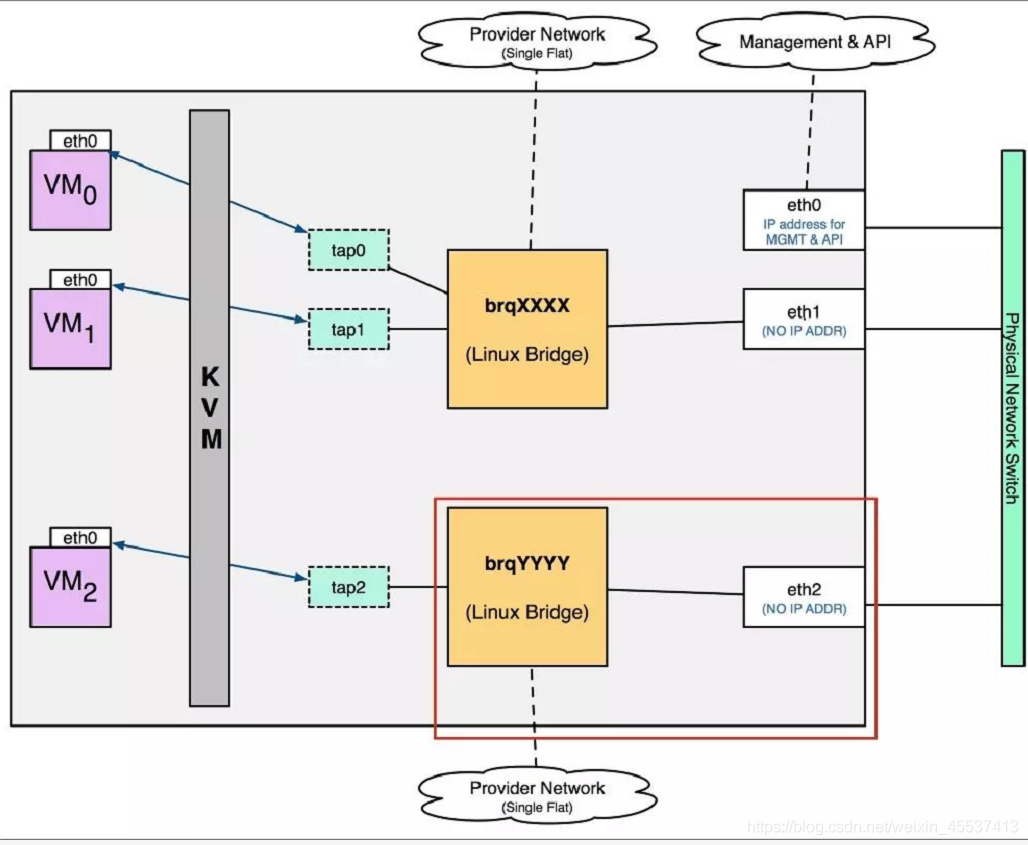
同样,配置文件中需要配置type_drivers的类型为flat网络,/etc/neutron/plugins/ml2/ml2_conf.ini,并设置普通租户创建的网络类型(admin用户可以指定网络类型)
[ml2]type_drivers = flattenant_network_types = flat......
此外还需要定义flat网络的标签(标签可以为任意字符串,需要保证控制和节点的命名保持一致,且后续在创建flat网络时也需要填写该标签),并制定标签与网卡之间的对应关系(各个计算节点的标签必须一致,但标签网卡对应关系可以不同。可以填写多个标签与各网卡之间一一对应,之间用逗号隔开,因此也就是对应多块网卡):

转载地址:http://kqrmz.baihongyu.com/